The PSNR block computes the peak signal-to-noise ratio, in decibels, between two images. This ratio is used as a quality measurement between the original and a compressed image. The higher the PSNR, the better the quality of the compressed, or reconstructed image.
The mean-square error (MSE) and the peak signal-to-noise ratio (PSNR) is used to compare image compression quality. The MSE represents the cumulative squared error between the compressed and the original image, whereas PSNR represents a measure of the peak error. The lower the value of MSE, the lower the error.
To compute the PSNR, the block first calculates the mean-squared error using the following equation:

In the previous equation, M and N are the number of rows and columns in the input images. Then the block computes the PSNR using the following equation:
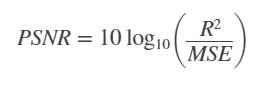
In the previous equation, R is the maximum fluctuation in the input image data type. For example, if the input image has a double-precision floating-point data type, then R is 1. If it has an 8-bit unsigned integer data type, R is 255, etc.
Computing PSNR for Color Images
Different approaches exist for computing the PSNR of a colour image. Because the human eye is most sensitive to luma information, you can compute the PSNR for colour images by converting the image to a colour space that separates the intensity (luma) channel, such as YCbCr. The Y (luma), in YCbCr represents a weighted average of R, G, and B. G is given the most weight, again because the human eye perceives it most easily. Compute the PSNR only on the luma channel.
import numpy
import math
import cv2
original = cv2.imread("original.png")
contrast = cv2.imread("photoshopped.png",1)
def psnr(img1, img2):
mse = numpy.mean( (img1 - img2) ** 2 )
if mse == 0:
return 100
PIXEL_MAX = 255.0
return 20 * math.log10(PIXEL_MAX / math.sqrt(mse))
d=psnr(original,contrast)
print(d)
You can use cv2.PSNR like this example:
import cv2
img1 = cv2.imread('img1.bmp')
img2 = cv2.imread('img2.bmp')
psnr = cv2.PSNR(img1, img2)

